Линейный поиск

Данный алгоритм сравнивает каждый элемент массива с ключом, предоставленным для поиска. Наш экспериментальный массив не упорядочен и, может сложиться ситуация, при которой отыскиваемое значение окажется первым в массиве. Но, в общем и целом, программа, реализующая линейный поиск, сравнит с ключом поиска половину элементов массива.

#include <iostream>
using namespace std;
int LinearSearch (int array[], int size, int key){
 for(int i=0;i < size;i++)
 if(array[i] == key)
 return i;
 return -1;
}
void main()
{
 const int arraySize=100;
 int a[arraySize], searchKey, element;
 for(int x=0;x < arraySize;x++)
 a[x]=2*x;
 // Следующая строка выводит на экран сообщение
 // Введите ключ поиска:
 cout<<"Please, enter the key: ";
 cin>>searchKey;
 element=LinearSearch(a, arraySize, searchKey);
 if(element!=-1)
 // Следующая строка выводит на экран сообщение
 // Найдено значение в элементе
 cout<<"\nThe key was found in element "<<
 element<<'\n';
 // Следующая строка выводит на экран сообщение
 // Значение не найдено
 else
 cout<<"\nValue not found ";
}

Заметим, что алгоритм линейного поиска отлично работает только для небольших или неупорядоченных массивов и является абсолютно надежным.

Двоичный поиск

Предположим, что переменные Lb и Ub содержат, соответственно, левую и правую границы отрезка массива, где находится нужный нам элемент. Поиск мы всегда будем начинать с анализа среднего элемента отрезка массива. Если искомое значение меньше среднего элемента, мы переходим к поиску в верхней половине отрезка, где все элементы меньше только что проверенного. Другими словами, значением Ub становится (M (средний элемент) –1) и на следующей итерации мы работаем с половиной массива. Таким образом, в результате каждой проверки мы вдвое сужаем область поиска. Так, в нашем примере, после первой итерации область поиска — всего лишь три элемента, после второй остается всего лишь один элемент. Таким образом, если длина массива равна 6, нам достаточно трех итераций, чтобы найти нужное число.

#include <iostream>
#include <stdlib.h>
#include <time.h>
using namespace std;

int BinarySearch (int A[], int Lb, int Ub, int Key)
{
 int M;
 while(1){
 M = (Lb + Ub)/2;
 if (Key < A[M])
 Ub = M - 1;
 else if (Key > A[M])
 Lb = M + 1;
 else
 return M;
 if (Lb > Ub)
 return -1;
 }
}
void main(){
 srand(time(NULL));
 const long SIZE=10;
 int ar[SIZE];
 int key,ind;
 // до сортировки
 for(int i=0;i < SIZE;i++){
 ar[i]=rand()%100;
 cout<< ar[i]<<"\t";
 }
 cout<<"\n\n";
 cout<<"Enter any digit:";
 cin>>key;
 ind=BinarySearch(ar,0,SIZE,key);
 cout<<"Index - "<< ind<<"\t";
 cout<<"\n\n";
}

Двоичный поиск — очень мощный метод. Посудите сами: например, длина массива равна 1023, после первого сравнения область сужается до 11 элементов, а после второй — до 255. Легко посчитать, что для поиска в массиве из 1023 элементов достаточно 10 сравнений.

Сортировка выбором

Идея данного метода состоит в том, чтобы создавать отсортированную последовательность путем присоединения к ней одного элемента за другим в правильном порядке. Сейчас, мы с вами попробуем построить готовую последовательность, начиная с левого конца массива. Алгоритм состоит из n последовательных шагов, начиная от нулевого и заканчивая (n–1). На i-м шаге выбираем наименьший из элементов a[i] ... a[n] и меняем его местами с a[i]. Последовательность шагов при n=5 изображена на рисунке ниже.

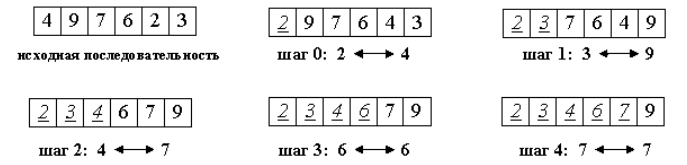
Вне зависимости от номера текущего шага i, последовательность a[0]...a[i] является упорядоченной. Таким образом, на шаге (n-1) вся последовательность, кроме a[n] оказывается отсортированной, а a[n] стоит на последнем месте по праву: все меньшие элементы уже ушли влево. Рассмотрим пример, реализующий данный метод:

#include <iostream>
#include <stdlib.h>
#include <time.h>
using namespace std;

template <class T> // Шаблоны смотрите в меню
void selectSort(T a[], long size) {
 long i, j, k;
 T x;
 for(i = 0; i < size; i++) { // i - номер текущего шага
 k=i;
 x=a[i];
 // цикл выбора наименьшего элемента
 for(j = i+1; j < size; j++)
 if(a[j] < x){
 k=j;
 x=a[j];
 // k - индекс наименьшего элемента
 }
 a[k]=a[i];
 a[i]=x; // меняем местами наименьший с a[i]
 }
}
void main(){
 srand(time(NULL));
 const long SIZE=10;
 int ar[SIZE];
 // до сортировки
 for(int i=0;i < SIZE;i++){
 ar[i]=rand()%100;
 cout<< ar[i]<<"\t";
 }
 cout<<"\n\n";
 selectSort(ar,SIZE);
 // после сортировки
 for(int i=0;i < SIZE;i++){
 cout<< ar[i]<<"\t";
 }
 cout<<"\n\n";
}

Для нахождения наименьшего элемента из n+1 рассматриваемый алгоритм совершает n сравнений. Таким образом, так как число обменов всегда будет меньше числа сравнений, время сортировки возрастает относительно количества элементов.

Алгоритм не использует дополнительной памяти: все операции происходят «на месте».

Пузырьковая сортировка

Идея метода состоит в следующем: шаг сортировки заключается в проходе снизу вверх по массиву. По пути просматриваются пары соседних элементов. Если элементы некоторой пары находятся в неправильном порядке, то меняем их местами. Для реализации расположим массив сверху вниз, от нулевого элемента — к последнему. После нулевого прохода по массиву «вверху» оказывается самый «легкий» элемент — отсюда аналогия с пузырьком. Следующий проход делается до второго сверху элемента, таким образом второй по величине элемент поднимается на правильную позицию.

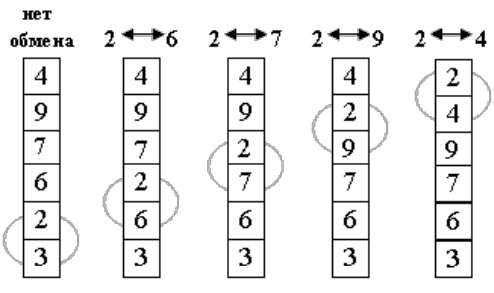
Делаем проходы по все уменьшающейся нижней части массива до тех пор, пока в ней не останется только один элемент. На этом сортировка заканчивается, так как последовательность упорядочена по возрастанию.

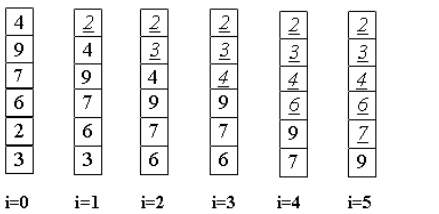
Пример:

#include <iostream>
#include <stdlib.h>
#include <time.h>
using namespace std;

template <class T> // Шаблоны смотрите в меню
void bubbleSort(T a[], long size){
 long i, j;
 T x;
 for(i=0;i<size;i++){ // i - номер прохода
 for(j=size-1;j>i;j--){ // внутренний цикл
 // прохода
 if(a[j-1]>a[j]){
 x=a[j-1];
 a[j-1]=a[j];
 a[j]=x;
 }
 }
 }
}
void main(){
 srand(time(NULL));
 const long SIZE=10;
 int ar[SIZE];

 // до сортировки

 for(int i=0; i < SIZE; i++){
 ar[i]=rand()%100;
 cout<< ar[i]<<"\t";
 }
 cout<<"\n\n";
 bubbleSort(ar,SIZE);
 // после сортировки
 for(int i=0; i < SIZE; i++){
 cout << ar[i] << "\t";
 }
 cout<<"\n\n";
}

Среднее число сравнений и обменов имеют квадратичный порядок роста, отсюда можно заключить, что алгоритм пузырька очень медлителен и малоэффективен. Тем не менее, у него есть громадный плюс: он прост и его можно по-всякому улучшать.

Сортировка вставками

Сортировка простыми вставками в чем-то похожа на методы изложенные в предыдущих разделах урока. Аналогичным образом делаются проходы по части массива, и аналогичным же образом в его начале «вырастает» отсортированная последовательность.

Однако в сортировке пузырьком или выбором можно было четко заявить, что на i-м шаге элементы a[0]...a[i] стоят на правильных местах и никуда более не переместятся. Здесь же подобное утверждение будет более слабым: последовательность a[0]...a[i] упорядочена. При этом по ходу алгоритма в нее будут вставляться все новые элементы.

Будем разбирать алгоритм, рассматривая его действия на i-м шаге. Как говорилось выше, последовательность к этому моменту разделена на две части: готовую a[0]...a[i] и неупорядоченную a[i+1]...a[n]. На следующем, (i+1)-м каждом шаге алгоритма берем a[i+1] и вставляем на нужное место в готовую часть массива. Поиск подходящего места для очередного элемента входной последовательности осуществляется путем последовательных сравнений с элементом, стоящим перед ним. В зависимости от результата сравнения элемент либо остается на текущем месте(вставка завершена), либо они меняются местами и процесс повторяется.

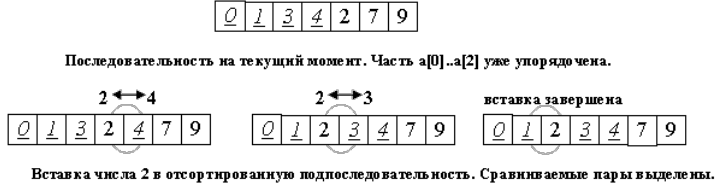
Таким образом, в процессе вставки мы «просеиваем» элемент x к началу массива, останавливаясь в случае, когда найден элемент, меньший x или достигнуто начало последовательности.

#include <iostream>
#include <stdlib.h>
#include <time.h>
using namespace std;

template <class T> // Шаблоны смотрите в меню
void insertSort(T a[], long size) {
 T x;
 long i, j;
 // цикл проходов, i - номер прохода
 for(i=0;i<size;i++){
 x=a[i];

 // поиск места элемента в готовой
 // последовательности
 for(j=i-1;j>=0&&a[j]>x;j--)
 // сдвигаем элемент направо,
 //пока не дошли
 a[j+1]=a[j];
 // место найдено, вставить элемент
 a[j+1] = x;
 }
}
void main(){
 srand(time(NULL));
 const long SIZE=10;
 int ar[SIZE];
 // до сортировки
 for(int i=0; i < SIZE; i++){
 ar[i]=rand()%100;
 cout<< ar[i]<<"\t";
 }
 cout<<"\n\n";
 shakerSort(ar,SIZE);
 // после сортировки
 for(int i=0; i < SIZE; i++){
 cout<< ar[i]<<"\t";
 }
 cout<<"\n\n";
}

Хорошим показателем сортировки является весьма естественное поведение: почти отсортированный массив будет досортирован очень быстро. Это, вкупе с устойчивостью алгоритма, делает метод хорошим выбором в соответствующих ситуациях.

Быстрая сортировка

Быстрая сортировка — была разработана около 40 лет назад и является наиболее широко применяемым и в принципе самым эффективным алгоритмом. Метод основан на разделении массива на части. Общая схема такова:

1. Из массива выбирается некоторый опорный элемент a[i].
2. Запускается функция разделения массива, которая перемещает все ключи, меньшие, либо равные a[i], слева от него, а все ключи, большие, либо равные a[i] — справа, теперь массив состоит из двух частей, причем элементы левой меньше элементов правой.
3. Если в подмассиве более двух элементов, рекурсивно запускаем для них ту же функцию.
4. В конце получится полностью отсортированная последовательность.
Рассмотрим алгоритм более детально.

Делим массив пополам

Входные данные: массив a[0]...a[N] и элемент p, по которому будет производиться разделение.

Введем два указателя: i и j. В начале алгоритма они указывают, соответственно, на левый и правый конец последовательности.

Будем двигать указатель i с шагом в 1 элемент по направлению к концу массива, пока не будет найден элемент a[i] >= p.

Затем аналогичным образом начнем двигать указатель j от конца массива к началу, пока не будет найден a[j] <= p.

Далее, если i <= j, меняем a[i] и a[j] местами и продолжаем двигать i, j по тем же правилам.

Повторяем шаг 3, пока i <= j.

Рассмотрим рисунок, где опорный элемент p = a[3].

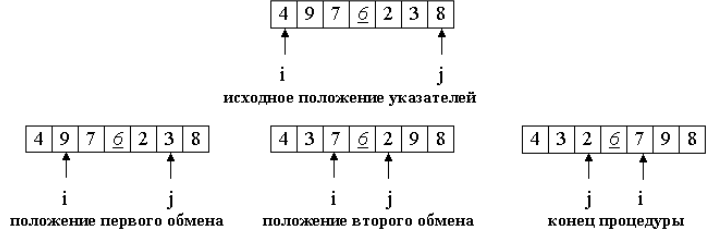
Массив разделился на две части: все элементы левой меньше либо равны p, все элементы правой — больше, либо равны p.

Пример программы:

#include <iostream>
#include <stdlib.h>
#include <time.h>
using namespace std;

template <class T> // Шаблоны смотрите в меню
void quickSortR(T a[], long N) {
 // На входе - массив a[], a[N] - его последний элемент.
 // поставить указатели на исходные места
 long i = 0, j = N;
 T temp, p;

 p = a[ N/2 ]; // центральный элемент
 // процедура разделения
 do {
 while ( a[i] < p ) i++;
 while ( a[j] > p ) j--;
 if (i <= j){
 temp = a[i];
 a[i] = a[j];
 a[j] = temp;
 i++;
 j--;
 }
 }
 while ( i<=j );
 // рекурсивные вызовы, если есть, что сортировать
 if ( j > 0 ) quickSortR(a, j);
 if ( N > i ) quickSortR(a+i, N-i);
}
void main(){
 srand(time(NULL));
 const long SIZE=10;
 int ar[SIZE];

 // до сортировки
 for(int i=0; i < SIZE; i++){
 ar[i]=rand()%100;
 cout<< ar[i]<<"\t";
 }
 cout<<"\n\n";
 quickSortR(ar,SIZE-1);
 // после сортировки
 for(int i=0; i < SIZE; i++){
 
 cout<< ar[i]<<"\t";
 }
 cout<<"\n\n";
}

Алгоритм рекурсии
1. Выбрать опорный элемент p — середину массива.
2. Разделить массив по этому элементу.
3. Если подмассив слева от p содержит более одного элемента, вызвать quickSortR для него.
4. Если подмассив справа от p содержит более одного элемента, вызвать quickSortR для него.